Image credit: [http://cursoronline.usal.es/viernes.html)
Introducción
¿Qué hace especial el trabajar con encuestas?
- Las encuestas incluyen una serie de items sobre un conjunto de observaciones: Parecen corresponderse con los datos ordenados (tibbles o data.frames)
¿Qué hace especial el trabajar con encuestas?
- Las encuestas incluyen una serie de items sobre un conjunto de observaciones: Parecen corresponderse con los datos ordenados (tibbles o data.frames)
Dos características los diferencian:
- En las encuestas son básicos los metadatos para poder trabajar con ellas, en particular los Metadatos de variable:
- Etiquetas de variable: Pregunta en el cuestionario, descripción de la variable.
- Etiquetas de valor: Redacción de las posibles respuestas. Tipos de no respuesta.
¿Qué hace especial el trabajar con encuestas?
- Las encuestas incluyen una serie de items sobre un conjunto de observaciones: Parecen corresponderse con los datos ordenados (tibbles o data.frames)
Dos características los diferencian:
- En las encuestas son básicos los metadatos para poder trabajar con ellas, en particular los Metadatos de variable:
- Etiquetas de variable: Pregunta en el cuestionario, descripción de la variable.
- Etiquetas de valor: Redacción de las posibles respuestas. Tipos de no respuesta.
- Las encuestas rara vez son muestras aleatorias (encuestas complejas). Si las tratamos como si fuera m.a. los resultados no son representativos:
- Las medias y porcentajes no se corresponden con los de la población.
- Los errores estándar no están bien calculados.
Soluciones
- En las encuestas son básicos los metadatos para poder trabajar con ellas, en particular los Metadatos de variable:
- Etiquetas de variable: Pregunta en el cuestionario, descripción de la variable.
- Etiquetas de valor: Redacción de las posibles respuestas. Tipos de no respuesta.
labelled data
Soluciones
- En las encuestas son básicos los metadatos para poder trabajar con ellas, en particular los Metadatos de variable:
- Etiquetas de variable: Pregunta en el cuestionario, descripción de la variable.
- Etiquetas de valor: Redacción de las posibles respuestas. Tipos de no respuesta.
labelled data
- Las encuestas rara vez son muestras aleatorias (encuestas complejas). Si lo tratamos como si fuera m.a. los resultados no son representativos:
- Las medias y porcentajes no se corresponden con los de la población.
Soluciones
- En las encuestas son básicos los metadatos para poder trabajar con ellas, en particular los Metadatos de variable:
- Etiquetas de variable: Pregunta en el cuestionario, descripción de la variable.
- Etiquetas de valor: Redacción de las posibles respuestas. Tipos de no respuesta.
labelled data
- Las encuestas rara vez son muestras aleatorias (encuestas complejas). Si lo tratamos como si fuera m.a. los resultados no son representativos:
- Las medias y porcentajes no se corresponden con los de la población.
Uso de pesos en tablas y modelos
Soluciones
- En las encuestas son básicos los metadatos para poder trabajar con ellas, en particular los Metadatos de variable:
- Etiquetas de variable: Pregunta en el cuestionario, descripción de la variable.
- Etiquetas de valor: Redacción de las posibles respuestas. Tipos de no respuesta.
labelled data
- Las encuestas rara vez son muestras aleatorias (encuestas complejas). Si lo tratamos como si fuera m.a. los resultados no son representativos:
- Las medias y porcentajes no se corresponden con los de la población.
Uso de pesos en tablas y modelos
- Los errores estándar no están bien calculados.
Paquete {survey}
Resumen de paquetes útiles para trabajar con encuestas:
| Paquete | ¿Para qué? |
|---|---|
| {haven} | Importar con etiquetas |
| {labelled} | Manejar etiquetas y variables. Transformar. |
| {sjlabelled} | Manejar etiquetas. Transformar variables |
| {sjmisc} | Describir variables. Tablas. |
| {expss} | Manejo variables. Presentar resultados. |
| {memisc} | Importar, transformar, presentar. |
| {sjPlot} | Tablas, gráficos publicables |
| {survey} | Análisis encuestas complejas |
Lectura de datos de encuesta
Formatos más habituales:
csvofwf+ Diseño de registro enxls: En desuso.{microdatosES}- Formatos internos de R:
rds:data=readRDS(...)RData:load(xxx.RData`)
- Formatos específicos de software estadístico:
sav: SPSSdat: STATA- SAS
Lectura de datos SPSS
| Paquete | Función | Resultado |
|---|---|---|
| foreign | read.spss |
list o data.frame con atributo labels |
| haven | read_sav |
tibble clase haven_labelled |
| sjlabelled | read_spss |
tibble clase labelled |
| memisc | spss.system.file + as.data.set |
data.set convertible a data.frame |
| eatGADS | import_spss |
GADSdat multinivel |
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Bajar datos
Variables de interés
Lectura
Más extenso aquí
Vamos a realizar un análisis completo (factores en el uso de anticonceptivos) de una encuesta compleja.
Empezamos por bajar los datos a nuestro disco.
library(tidyverse)urlbase="http://iinei.inei.gob.pe/iinei/srienaho/descarga/SPSS/"# Generamos una tiabla con las extensiones y # contenidos de los ficherosficheros= tribble(~contenido,~fichero, "DatosBasicos","691-Modulo66.zip", "Nacimientos","691-Modulo67.zip", "Nupcialidad","691-Modulo71.zip" )# Bajamos a la carpeta data aprovechando las# funciones del paquete purrr del tidyverseficheros %>% pwalk(~download.file(paste0(urlbase,.y), destfile=paste0("data/",.x,".zip"),mode="wb"))Recordatorio: %>%, el operador después, define operaciones de forma secuencial. En RStudio: CTR+MAYUSC+M.
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Bajar datos
Variables de interés
Lectura
Más extenso aquí
varsel=tribble(~Variable,~Significado,~Módulo,~Fichero,~Tipo, "V313","Uso actual de método","RE223132","Nacimientos","Explicada", "V218","Hijos vivos","RE223132","Nacimientos","Explicativa", "V106","Nivel educativo","REC0111","DatosBasicos","Explicativa", "V012","Edad actual","REC0111","DatosBasicos","Explicativa", "V013","Grupo de edad","REC0111","DatosBasicos","Explicativa", "V025","Lugar de residencia","REC0111","DatosBasicos","Explicativa", "V501","Estado civil","RE516171","Nupcialidad","Explicativa", "V213","Embarazada","RE223132","Nacimientos","Selección", "V536","Actividad sexual","RE516171","Nupcialidad","Selección", "CASEID","Identificación indiv","Todos","Todos","Técnica", "V022","Estrato","REC0111","DatosBasicos","Técnica", "V004","Unidad de área final","REC0111","DatosBasicos","Técnica", "V005","Ponderación (mujer)","REC0111","DatosBasicos","Técnica")| Variable | Significado | Fichero | Tipo |
|---|---|---|---|
| V313 | Uso actual de método | Nacimientos | Explicada |
| V218 | Hijos vivos | Nacimientos | Explicativa |
| V106 | Nivel educativo | DatosBasicos | Explicativa |
| V012 | Edad actual | DatosBasicos | Explicativa |
| V013 | Grupo de edad | DatosBasicos | Explicativa |
| V025 | Lugar de residencia | DatosBasicos | Explicativa |
| V501 | Estado civil | Nupcialidad | Explicativa |
| V213 | Embarazada | Nacimientos | Selección |
| V536 | Actividad sexual | Nupcialidad | Selección |
| CASEID | Identificación indiv | Todos | Técnica |
| V022 | Estrato | DatosBasicos | Técnica |
| V004 | Unidad de área final | DatosBasicos | Técnica |
| V005 | Ponderación (mujer) | DatosBasicos | Técnica |
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Bajar datos
Variables de interés
Lectura
Más extenso aquí
temp <- tempfile()varsel %>% filter(Fichero!="Todos") %>% pull(Fichero) %>% unique() %>% paste0("data/",.,".zip") %>% walk(unzip,junkpaths=TRUE,exdir=temp) #Descomprime todo en la misma carpeta.m = varsel %>% filter(Módulo!="Todos") %>% pull(Módulo) %>% unique()dir(temp) %>% as_tibble() %>% filter(value %>% str_detect(.m %>% paste(collapse="|"))) %>% mutate(value=paste(temp,value,sep="/")) %>% pull(value) %>% file.copy("data/")rm(.m)Las funciones del {tidyverse} son utilísimas para manipular tiablas
Esta encuesta está bien definida, y {haven} funciona perfectamente.
Aquí podéis ver otro ejemplo, con una encuesta del INE que tiene variables con problemas y hay que utilizar otros alternativas de lectura.
Leemos directamente desde el sav el archivo de datos básicos, al que le pegamos los datos de nacimientos y nupcialidad.
Este es un caso complejo porque los datos están en varios ficheros. Si sólo hay uno es muy sencillo.
library(haven)DHS=read_sav("data/REC0111.sav") %>% left_join(read_sav("data/RE223132.sav"),by=c("ID1","CASEID")) %>% left_join(read_sav("data/RE516171.sav"),by=c("ID1","CASEID"))class(DHS) # Se trata de una "tiabla"## [1] "tbl_df" "tbl" "data.frame"dim(DHS) # Con estas dimensiones:## [1] 38335 361Trabajando con etiquetas: labelled data
Objetos labelled en R
- Hay dos clases en R con etiquetas, compatibles entre sí,
labelledyhaven-labelled. - Ambas tienen etiquetas de variable (variable labels) y etiquetas de valores (value labels).
- Desafortunadamente la mayoría de los paquetes de R no entienden las variables con etiquetas.
- Aparentemente son variables numéricas, pero cada valor tiene asignado un código.
- Podemos trabajar con los paquetes que entienden las etiquetas, o convertirlas a factores o variables numéricas.
# install.packages("sjmisc")DHS %>% sjmisc::find_var("Edad") %>% knitr::kable()| col.nr | var.name | var.label |
|---|---|---|
| 13 | V012 | Edad actual - entrevistada |
| 14 | V013 | Edad actual por grupos de 5 años |
| 75 | V152 | Edad del jefe del hogar |
| 117 | V212 | Edad del entrevistado al primer nacimiento |
| 159 | V320 | Edad en la esterilización |
| 290 | V511 | Edad al primer matrimonio |
| 293 | V525 | Edad en la primera relación sexual |
| 298 | V531 | Edad en la primera relación sexual (imp) |
| 344 | V730 | Edad del esposo/compañero |
# install.packages("labelled")labelled::look_for(DHS,"hijos") %>% knitr::kable()| pos | variable | label | col_type | class | type | levels | value_labels | na_values | na_range | unique_values | n_na | range |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 107 | V202 | ¿Cuántos hijos viven con usted? | dbl | numeric | double | NULL | NULL | NULL | NULL | 9 | 1413 | 0, 7 |
| 109 | V204 | ¿Cuántos hijos no están viviendo con usted? | dbl | numeric | double | NULL | NULL | NULL | NULL | 8 | 1413 | 0, 6 |
| 111 | V206 | ¿Cuántos hijos han muerto? | dbl | numeric | double | NULL | NULL | NULL | NULL | 6 | 1413 | 0, 4 |
| 124 | V219 | Número total de hijos vivos incluido el embarazo actual | dbl | numeric | double | NULL | NULL | NULL | NULL | 15 | 1413 | 0, 13 |
| 125 | V220 | Número total de hijos vivos incluido el embarazo actual (6, si es mayor de 6) | dbl+lbl | haven_labelled, vctrs_vctr , double | double | NULL | 6 | NULL | NULL | 8 | 1413 | 0, 6 |
| 150 | V310 | Cuantas hijas e hijos tenía cuando empezó a usar el primer método para no quedar embarazada | dbl | numeric | double | NULL | NULL | NULL | NULL | 13 | 9415 | 0, 12 |
| 151 | V311 | Cuantas hijas e hijos tenía cuando empezó a usar el primer método (Grupos) | dbl+lbl | haven_labelled, vctrs_vctr , double | double | NULL | 4, 5 | NULL | NULL | 7 | 5024 | 0, 5 |
| 310 | V605 | Deseo de tener más hijos | dbl+lbl | haven_labelled, vctrs_vctr , double | double | NULL | 1, 2, 3, 4, 5, 6, 7 | NULL | NULL | 8 | 5024 | 1, 7 |
| 314 | V621 | Piensa que su esposo/compañero desea el mismo número de hijos | dbl+lbl | haven_labelled, vctrs_vctr , double | double | NULL | 1, 2, 3, 8 | NULL | NULL | 5 | 18367 | 1, 8 |
| 319 | V627 | Número ideal de hijos | dbl+lbl | haven_labelled, vctrs_vctr , double | double | NULL | 96 | NULL | NULL | 14 | 5024 | 0, 96 |
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Describir variables
Funciones genéricas
Etiquetas
Tabulaciones
Estadísticos
Más extenso aquí
Seleccionamos nuestra variable de interés, V313, la variable de uso de anticonceptivos.
Obviamente no es una variable cuantitativa, pero los datos labelled están almacenados como número, con las etiquetas como atributos.
class(DHS$V313) #Clase del objeto## [1] "haven_labelled" "vctrs_vctr" "double"summary(DHS$V313) #Resumen. Función genérica, pero sin método para labelled## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's ## 0.000 0.000 2.000 1.673 3.000 3.000 5024Aunque no sea numérico,
summaryno se da cuenta. Eso les pasa a muchas funciones.
Es básico trabajar con funciones que entiendan los datos labelled o transformarlas a factores o variables cuantitativas.
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Describir variables
Funciones genéricas
Etiquetas
Tabulaciones
Estadísticos
Más extenso aquí
Tanto sjlabelled como labelled y expss tienen funciones.
# install.packages("sjlabelled")sjlabelled::get_label(DHS$V313) #Etiqueta de variable## [1] "Uso actual por tipo de método"sjlabelled::get_labels(DHS$V313) #Etiquetas de valor## [1] "No hay método" "Método folclórico" ## [3] "Método tradicional" "Método moderno"# install.packages("labelled")labelled::var_label(DHS$V313) #Etiqueta de variable## [1] "Uso actual por tipo de método"labelled::val_labels(DHS$V313) # Etiquetas de valor## No hay método Método folclórico Método tradicional ## 0 1 2 ## Método moderno ## 3# install.packages("expss")expss::var_lab(DHS$V313) #Etiqueta de variable## [1] "Uso actual por tipo de método"expss::val_lab(DHS$V313) # Etiquetas de valor## No hay método Método folclórico Método tradicional ## 0 1 2 ## Método moderno ## 3Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Describir variables
Funciones genéricas
Etiquetas
Tabulaciones
Estadísticos
Más extenso aquí
Tanto sjmisc como memisc o el tidyverse tienen funciones.
# install.packages("sjmisc")sjmisc::frq(DHS$V313) #Tabulación simple## ## Uso actual por tipo de método (x) <numeric>## # total N=38335 valid N=33311 mean=1.67 sd=1.39## ## Value | Label | N | Raw % | Valid % | Cum. %## -------------------------------------------------------------## 0 | No hay método | 13017 | 33.96 | 39.08 | 39.08## 1 | Método folclórico | 188 | 0.49 | 0.56 | 39.64## 2 | Método tradicional | 4762 | 12.42 | 14.30 | 53.94## 3 | Método moderno | 15344 | 40.03 | 46.06 | 100.00## <NA> | <NA> | 5024 | 13.11 | <NA> | <NA># install.packages("memisc")memisc::codebook(DHS$V313) # Si hay más variables, de todas.## ============================================================## ## DHS$V313 'Uso actual por tipo de método'## ## ------------------------------------------------------------## ## Storage mode: double## Measurement: undefined## ## Values and labels N Valid Total## ## 0 'No hay método' 13017 39.1 34.0## 1 'Método folclórico' 188 0.6 0.5## 2 'Método tradicional' 4762 14.3 12.4## 3 'Método moderno' 15344 46.1 40.0## NA M 5024 13.1Las versiones antiguas no reconocían etiquetas. ¡Ahora sí!
DHS %>% count(V313) %>%mutate(`% (todos)`=n/sum(n)*100,`% (validos)`=n/(sum(n)-last(n))*100)## # A tibble: 5 x 4## V313 n `% (todos)` `% (validos)`## * <dbl+lbl> <int> <dbl> <dbl>## 1 0 [No hay método] 13017 34.0 39.1 ## 2 1 [Método folclórico] 188 0.490 0.564## 3 2 [Método tradicional] 4762 12.4 14.3 ## 4 3 [Método moderno] 15344 40.0 46.1 ## 5 NA 5024 13.1 15.1Ejemplo:
Describir variables cuantitativas
Funciones genéricas
Etiquetas
Tabulaciones
Estadísticos
Más extenso aquí
sjmisc::descr(DHS %>% select(V201,V218))## ## ## Basic descriptive statistics## ## var type label n NA.prc mean sd## V201 numeric Total de niños nacidos 36922 3.69 1.78 1.75## V218 numeric Número de niños vivos 36922 3.69 1.73 1.67## se md trimmed range iqr skew## 0.01 1 1.54 13 (0-13) 3 1.33## 0.01 1 1.51 13 (0-13) 3 1.23# install.packages("Hmisc")Hmisc::describe(DHS %>% select(V201)) # Si hay más variables, de todas.## DHS %>% select(V201) ## ## 1 Variables 38335 Observations## ------------------------------------------------------------## V201 : Total de niños nacidos Format:F2.0 ## n missing distinct Info Mean Gmd ## 36922 1413 14 0.953 1.782 1.837 ## .05 .10 .25 .50 .75 .90 ## 0 0 0 1 3 4 ## .95 ## 5 ## ## lowest : 0 1 2 3 4, highest: 9 10 11 12 13## ## Value 0 1 2 3 4 5 6 7## Frequency 10565 7950 8074 5099 2583 1294 642 328## Proportion 0.286 0.215 0.219 0.138 0.070 0.035 0.017 0.009## ## Value 8 9 10 11 12 13## Frequency 187 99 66 22 10 3## Proportion 0.005 0.003 0.002 0.001 0.000 0.000## ------------------------------------------------------------# install.packages("qwraps2")options(qwraps2_markup = "markdown")qwraps2::summary_table(DHS %>% select(V201,V218))| DHS %>% select(V201, V218) (N = 38,335) | |
|---|---|
| Total de niños nacidos | |
| minimum | 0.00 |
| median (IQR) | 1.00 (0.00, 3.00) |
| mean (sd) | 1.78 ± 1.75 |
| maximum | 13.00 |
| Unknown/Missing | 1,413 (3.69%) |
| Número de niños vivos | |
| minimum | 0.00 |
| median (IQR) | 1.00 (0.00, 3.00) |
| mean (sd) | 1.73 ± 1.67 |
| maximum | 13.00 |
| Unknown/Missing | 1,413 (3.69%) |
Encuestas complejas: Uso de pesos en tabulaciones y modelos
¿Por qué es necesario usar pesos?
La gran mayoría de encuestas NO son una muestra aleatoria simple. Suelen ser muestreo aleatorio dentro de unidades primarias de muestreo.
Éstas quedan definidas por los:
Estratos: Subpoblaciones naturales que queremos estudiar (ej: sexo, edad, CCAA).
Conglomerados: Unidades definidas dentro de cada estrato seleccionadas por muestreo.
El resultado es que las distintas unidades no tienen la misma probabilidad de ser seleccionadas.
Para obtener estimaciones representativas de la población debemos dar más peso a las observaciones con menor probabilidad de inclusión.
Tipos de pesos
Peso de diseño: Calculado como la inversa de la probabilidad de selección.
Peso postestratificación: Ajustan por la tasa de no respuesta dentro de cada unidad primaria de muestreo.
Peso normalizado: Peso tipificado para tener media igual a 1.
Muchos procedimientos estadísticos en R (ej:
glm), asumen que, si hay pesos, representan el número de observaciones. Es necesario usar pesos normalizados para no sobrevalorar la precisión teniendo en cuenta las distintas probabilidad de selección.La DHS proporciona pesos postestratificación normalizados
DHS = DHS %>% mutate(peso=V005/1000000)DHS %>% sjmisc::descr(peso)## ## ## Basic descriptive statistics## ## var type label n NA.prc mean sd## peso numeric Factor de ponderacion 38335 0 0.96 1.67## se md trimmed range iqr skew## 0.01 0.45 0.61 28.92 (0-28.92) 0.7456075 4.7Distribución de los pesos en el ejemplo
Los pesos normalizados representan cuán infrarrepresentadas están las mujeres como la entrevistada.
DHS %>% ggplot(aes(y=peso,x=0),alpha=0.7) + geom_jitter(size=0.1) + geom_violin(fill="magenta") + scale_y_log10() + scale_x_discrete(labels = NULL, breaks = NULL) + labs(x = "") + theme_minimal(20)Algunas mujeres están 10 veces sobrerrepresentadas y otras 10 veces infrarrepresentadas. Muy lejos del muestreo aleatorio.
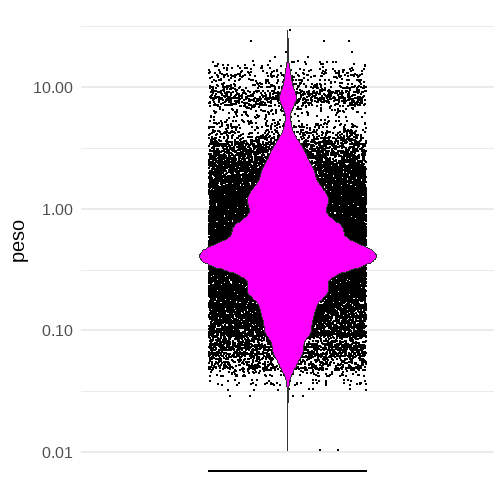
Sesgos al no ponderar si la variable de interés se relaciona con el peso
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Tablas ponderadas
Una variable
Tabulaciones cruzadas
Modelos
Más extenso aquí
Tanto sjmisc como expss y el tidyverse tienen funciones.
# install.packages("sjmisc")sjmisc::frq(DHS$V313) #Tabulación simple## ## Uso actual por tipo de método (x) <numeric>## # total N=38335 valid N=33311 mean=1.67 sd=1.39## ## Value | Label | N | Raw % | Valid % | Cum. %## -------------------------------------------------------------## 0 | No hay método | 13017 | 33.96 | 39.08 | 39.08## 1 | Método folclórico | 188 | 0.49 | 0.56 | 39.64## 2 | Método tradicional | 4762 | 12.42 | 14.30 | 53.94## 3 | Método moderno | 15344 | 40.03 | 46.06 | 100.00## <NA> | <NA> | 5024 | 13.11 | <NA> | <NA>sjmisc::frq(DHS,V313,weights=peso) #Tabulación ponderada## ## Uso actual por tipo de método (V313) <numeric>## # total N=33381 valid N=33381 mean=1.44 sd=1.41## ## Value | Label | N | Raw % | Valid % | Cum. %## -------------------------------------------------------------## 0 | No hay método | 15916 | 47.68 | 47.68 | 47.68## 1 | Método folclórico | 102 | 0.31 | 0.31 | 47.99## 2 | Método tradicional | 4237 | 12.69 | 12.69 | 60.68## 3 | Método moderno | 13126 | 39.32 | 39.32 | 100.00## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>Grandes diferencias, por ejemplo en las no usuarias.
Requiere más código, pero permite controlar todo lo que se pone en las tablas, y permite pesos.
library(expss)DHS %>% tab_cells(V313) %>% tab_weight(peso) %>% tab_stat_cpct() %>% tab_pivot()| #Total | |
|---|---|
| Uso actual por tipo de método | |
| No hay método | 47.7 |
| Método folclórico | 0.3 |
| Método tradicional | 12.7 |
| Método moderno | 39.3 |
| #Total cases | 33311 |
DHS %>% count(V313,wt=peso) %>% mutate(`% (todos)`=n/sum(n)*100, `% (validos)`=n/(sum(n)-last(n))*100)## # A tibble: 5 x 4## V313 n `% (todos)` `% (validos)`## * <dbl+lbl> <dbl> <dbl> <dbl>## 1 0 [No hay método] 15916. 43.1 47.7 ## 2 1 [Método folclórico] 102. 0.277 0.306## 3 2 [Método tradicional] 4237. 11.5 12.7 ## 4 3 [Método moderno] 13126. 35.6 39.3 ## 5 NA 3540. 9.59 10.6Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Tablas ponderadas
Una variable
Tabulaciones cruzadas
Modelos
Más extenso aquí
DHS %>% group_by(V025) %>% sjmisc::frq(V313,weights=peso) # ponderada## ## Uso actual por tipo de método (V313) <numeric>## # grouped by: Urbano## # total N=27574 valid N=27574 mean=1.42 sd=1.42## ## Value | Label | N | Raw % | Valid % | Cum. %## -------------------------------------------------------------## 0 | No hay método | 13473 | 48.86 | 48.86 | 48.86## 1 | Método folclórico | 48 | 0.17 | 0.17 | 49.04## 2 | Método tradicional | 3130 | 11.35 | 11.35 | 60.39## 3 | Método moderno | 10923 | 39.61 | 39.61 | 100.00## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>## ## ## Uso actual por tipo de método (V313) <numeric>## # grouped by: Rural## # total N=5807 valid N=5807 mean=1.53 sd=1.36## ## Value | Label | N | Raw % | Valid % | Cum. %## ------------------------------------------------------------## 0 | No hay método | 2443 | 42.07 | 42.07 | 42.07## 1 | Método folclórico | 54 | 0.93 | 0.93 | 43.00## 2 | Método tradicional | 1107 | 19.06 | 19.06 | 62.06## 3 | Método moderno | 2203 | 37.94 | 37.94 | 100.00## <NA> | <NA> | 0 | 0.00 | <NA> | <NA>DHS %>% sjmisc::flat_table(V313,V025, margin="col",weights=peso)## V025 Urbano Rural## V313 ## No hay método 48.86 42.07## Método folclórico 0.17 0.93## Método tradicional 11.35 19.06## Método moderno 39.61 37.94Por defecto representa recuentos. Podemos utilizar porcentajes de fila ("row"), columna ("col") o celda ("cell").
library(expss)DHS %>% tab_cells(V313) %>% tab_cols(V025) %>% tab_weight(peso) %>% tab_stat_cpct() %>% tab_pivot()| Tipo de lugar de residencia | ||
|---|---|---|
| Urbano | Rural | |
| Uso actual por tipo de método | ||
| No hay método | 48.9 | 42.1 |
| Método folclórico | 0.2 | 0.9 |
| Método tradicional | 11.4 | 19.1 |
| Método moderno | 39.6 | 37.9 |
| #Total cases | 23873 | 9438 |
DHS %>% group_by(V025) %>% count(V313,wt=peso) %>% mutate(`% (todos)`=n/sum(n)*100, `% (validos)`=n/(sum(n)-last(n))*100) %>% knitr::kable()| V025 | V313 | n | % (todos) | % (validos) |
|---|---|---|---|---|
| 1 | 0 | 13473.30212 | 44.6345592 | 48.8618408 |
| 1 | 1 | 47.91835 | 0.1587446 | 0.1737791 |
| 1 | 2 | 3130.19963 | 10.3697727 | 11.3518805 |
| 1 | 3 | 10922.86262 | 36.1854246 | 39.6124995 |
| 1 | NA | 2611.52481 | 8.6514989 | 9.4708712 |
| 2 | 0 | 2443.07359 | 36.2678698 | 42.0690825 |
| 2 | 1 | 54.31568 | 0.8063260 | 0.9353016 |
| 2 | 2 | 1106.50080 | 16.4262047 | 19.0536517 |
| 2 | 3 | 2203.39986 | 32.7098700 | 37.9419642 |
| 2 | NA | 928.90274 | 13.7897295 | 15.9954601 |
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
Tablas ponderadas
Una variable
Tabulaciones cruzadas
Modelos
Más extenso aquí
mod1=glm(I(V313==3)~V025,family=binomial, data=DHS,weights=peso)summary(mod1)## ## Call:## glm(formula = I(V313 == 3) ~ V025, family = binomial, data = DHS, ## weights = peso)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -4.8983 -0.7358 -0.3379 0.8611 7.3190 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -0.35126 0.03657 -9.604 <2e-16 ***## V025 -0.07037 0.02971 -2.368 0.0179 * ## ---## Signif. codes: ## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 44742 on 33310 degrees of freedom## Residual deviance: 44737 on 33309 degrees of freedom## (5024 observations deleted due to missingness)## AIC: 40087## ## Number of Fisher Scoring iterations: 3mod2=use_labels(DHS, glm(I(V313==3)~V025,family=binomial,weights=peso))summary(mod2)## ## Call:## glm(formula = I(`Uso actual por tipo de método` == 3) ~ `Tipo de lugar de residencia V025`, ## family = binomial, weights = `Factor de ponderacion peso`)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -4.8983 -0.7358 -0.3379 0.8611 7.3190 ## ## Coefficients:## Estimate Std. Error## (Intercept) -0.35126 0.03657## `Tipo de lugar de residencia V025` -0.07037 0.02971## z value Pr(>|z|) ## (Intercept) -9.604 <2e-16 ***## `Tipo de lugar de residencia V025` -2.368 0.0179 * ## ---## Signif. codes: ## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 44742 on 33310 degrees of freedom## Residual deviance: 44737 on 33309 degrees of freedom## (5024 observations deleted due to missingness)## AIC: 40087## ## Number of Fisher Scoring iterations: 3sjPlot::tab_model(mod1,dv.labels="Uso anticonceptivos modernos")| Uso anticonceptivos modernos | |||
|---|---|---|---|
| Predictors | Odds Ratios | CI | p |
| (Intercept) | 0.70 | 0.66 – 0.76 | <0.001 |
| Tipo de lugar de residencia |
0.93 | 0.88 – 0.99 | 0.018 |
| Observations | 33311 | ||
Produce tablas de resultados que usan etiquetas, y muy configurable.
El problema es que con encuestas complejas los errores estándar no están bien calculados: no es una muestra aleatoria.
Encuestas complejas: Cálculo apropiado de errores estándar. El paquete {survey}
¿Por qué están mal calculados los errores estándar?
- Dentro de cada unidad primaria de muestreo habrá menos variabilidad que en la población en general.
- Si no lo tenemos en cuenta, en general estaremos subestimando la varianza.
- El estudio de la varianza entre grupos me permitirá estimar la variabilidad correcta.
¿Por qué están mal calculados los errores estándar?
- Dentro de cada unidad primaria de muestreo habrá menos variabilidad que en la población en general.
- Si no lo tenemos en cuenta, en general estaremos subestimando la varianza.
- El estudio de la varianza entre grupos me permitirá estimar la variabilidad correcta.
¿Qué hacer?
- En cada modelo: Uso de matriz de varianzas-covarianzas
vcovCLdefiniendo la variable de conglomerados.
¿Por qué están mal calculados los errores estándar?
- Dentro de cada unidad primaria de muestreo habrá menos variabilidad que en la población en general.
- Si no lo tenemos en cuenta, en general estaremos subestimando la varianza.
- El estudio de la varianza entre grupos me permitirá estimar la variabilidad correcta.
¿Qué hacer?
En cada modelo: Uso de matriz de varianzas-covarianzas
vcovCLdefiniendo la variable de conglomerados.En general: Especificar con
{survey}la estructura de la encuesta, y usar sus funciones especializadas.
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
{survey}
Diseño de la encuesta
IC de proporciones
Tabulaciones cruzadas
Modelos
Más extenso aquí
Hacemos las manipulaciones de variables antes de crear el diseño. De otro modo es más complicado (aunque podéis mirar {srvyr}, y luego veremos un ejemplo de mutación directamente en un objeto survey.design )
NOTA: La opción `out="v" sirve para tablas con formato html.
DHS=DHS %>% mutate(moderno=factor((V313==3), labels=c("No","Si")))DHS %>% sjmisc::frq(moderno,weights=peso,out="v")| val | label | frq | raw.prc | valid.prc | cum.prc | |
|---|---|---|---|---|---|---|
| No | 20255 | 60.68 | 60.68 | 60.68 | ||
| Si | 13126 | 39.32 | 39.32 | 100 | ||
| NA | NA | 0 | 0 | NA | NA | |
| total N=33381 · valid N=33381 · x̄=1.39 · σ=0.49 | ||||||
Tenemos que declarar la variable con los nombres de los conglomerados, ids, la de estratos strata, y los pesos weights.
#install.packages("survey")library(survey)disDHS=svydesign(ids=~V021, strata=~V022, weights=~peso, data=DHS %>% filter(peso>0,!is.na(moderno)), nest=TRUE)summary(disDHS)## Stratified 1 - level Cluster Sampling design (with replacement)## With (3252) clusters.## svydesign(ids = ~V021, strata = ~V022, weights = ~peso, data = DHS %>% ## filter(peso > 0, !is.na(moderno)), nest = TRUE)## Probabilities:## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 0.03457 0.98965 2.16821 3.36628 3.82383 94.97578 ## Stratum Sizes: ## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15## obs 11 42 31 33 47 80 75 125 86 710 23 95 164 117 97## design.PSU 2 4 4 4 5 8 8 13 9 62 4 11 15 12 10## actual.PSU 2 4 4 4 5 8 8 13 9 62 4 11 15 12 10## 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30## obs 33 24 39 41 27 475 33 38 54 40 22 84 65 41 68## design.PSU 4 2 5 4 3 40 4 4 6 4 3 8 6 5 7## actual.PSU 4 2 5 4 3 40 4 4 6 4 3 8 6 5 7## 31 32 33 34 35 36 37 38 39 40 41 42 43 44## obs 575 100 168 237 216 154 27 49 21 62 80 123 37 79## design.PSU 58 11 18 23 20 15 3 6 2 6 8 12 4 8## actual.PSU 58 11 18 23 20 15 3 6 2 6 8 12 4 8## 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59## obs 99 161 59 60 56 79 26 102 505 20 34 22 57 36 43## design.PSU 9 13 6 6 6 8 3 12 50 2 3 2 5 4 6## actual.PSU 9 13 6 6 6 8 3 12 50 2 3 2 5 4 6## 60 61 62 63 64 65 66 67 68 69 70 71 72 73## obs 29 69 32 24 799 152 248 429 201 270 23 61 77 84## design.PSU 4 7 3 3 66 19 28 42 17 24 4 8 9 9## actual.PSU 4 7 3 3 66 19 28 42 17 24 4 8 9 9## 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88## obs 54 26 55 52 47 41 509 14 63 40 20 37 49 65 751## design.PSU 6 3 6 6 6 4 46 2 6 4 2 4 5 7 75## actual.PSU 6 3 6 6 6 4 46 2 6 4 2 4 5 7 75## 89 90 91 92 93 94 95 96 97 98 99 100 101 102## obs 65 64 63 74 36 42 113 37 20 779 44 65 98 68## design.PSU 7 7 7 7 4 5 11 4 2 64 5 8 9 7## actual.PSU 7 7 7 7 4 5 11 4 2 64 5 8 9 7## 103 104 105 106 107 108 109 110 111 112 113 114## obs 44 15 134 232 222 284 123 17 67 80 108 55## design.PSU 4 2 12 22 22 24 9 2 8 9 10 5## actual.PSU 4 2 12 22 22 24 9 2 8 9 10 5## 115 116 117 118 119 120 121 122 123 124 125 126## obs 115 56 26 162 102 389 52 94 136 150 95 59## design.PSU 13 6 3 16 10 32 7 11 14 13 9 7## actual.PSU 13 6 3 16 10 32 7 11 14 13 9 7## 127 128 129 130 131 132 133 134 135 136 137 138## obs 27 119 54 135 312 69 100 167 145 125 41 103## design.PSU 3 11 6 13 23 8 10 16 13 9 4 10## actual.PSU 3 11 6 13 23 8 10 16 13 9 4 10## 139 140 141 142 143 144 145 146 147 148 149 150## obs 85 167 112 225 212 388 898 982 704 133 316 301## design.PSU 8 16 12 16 43 49 93 92 63 15 30 28## actual.PSU 8 16 12 16 43 49 93 92 63 15 30 28## 151 152 153 154 155 156 157 158 159 160 161 162## obs 35 154 277 83 215 136 147 88 16 60 44 98## design.PSU 4 14 26 8 17 11 11 8 2 4 3 10## actual.PSU 4 14 26 8 17 11 11 8 2 4 3 10## 163 164 165 166 167 168 169 170 171 172 173 174## obs 76 432 102 210 248 92 62 107 287 76 78 121## design.PSU 8 32 12 24 25 9 7 14 26 8 9 13## actual.PSU 8 32 12 24 25 9 7 14 26 8 9 13## 175 176 177 178 179 180 181 182 183 184 185 186## obs 64 137 74 200 61 132 134 67 101 59 41 27## design.PSU 6 15 9 23 6 14 18 8 11 6 5 3## actual.PSU 6 15 9 23 6 14 18 8 11 6 5 3## 187 188 189 190 191 192 193 194 195 196 197 198## obs 205 94 102 339 22 44 63 95 113 81 188 212## design.PSU 22 11 13 34 2 4 6 8 10 8 16 18## actual.PSU 22 11 13 34 2 4 6 8 10 8 16 18## 199 200 201 202 203 204 205 206 207 208 209 210## obs 263 259 11 26 21 23 20 16 71 101 71 136## design.PSU 25 22 2 3 2 2 2 2 8 10 7 14## actual.PSU 25 22 2 3 2 2 2 2 8 10 7 14## 211 212 213 214 215 216 217 218 219 220 221 222## obs 492 18 96 108 81 64 50 83 59 106 191 419## design.PSU 53 2 9 10 6 6 5 8 6 11 19 32## actual.PSU 53 2 9 10 6 6 5 8 6 11 19 32## 223 224 225 226 228 229 230 231 232 233 234 235## obs 125 255 379 310 24 130 30 88 182 198 95 53## design.PSU 14 27 35 28 5 14 4 9 16 18 10 5## actual.PSU 14 27 35 28 5 14 4 9 16 18 10 5## 236 237 238 239 240 241 242 243 244 245 246 247## obs 79 140 235 90 119 35 105 201 258 341 21 57## design.PSU 7 14 23 9 10 4 9 19 21 29 2 6## actual.PSU 7 14 23 9 10 4 9 19 21 29 2 6## 248 249## obs 69 275## design.PSU 7 22## actual.PSU 7 22## Data variables:## [1] "ID1" "HHID" "CASEID" ## [4] "V001" "V002" "V003" ## [7] "V004" "V007" "V008" ## [10] "V009" "V010" "V011" ## [13] "V012" "V013" "V014" ## [16] "V015" "V017" "V018" ## [19] "V019" "V019A" "V020" ## [22] "V021" "V023" "V024" ## [25] "V025" "V026" "V027" ## [28] "V028" "V029" "V030" ## [31] "V031" "V032" "V033" ## [34] "V034" "V040" "V042" ## [37] "V043" "V044" "V000" ## [40] "Q105DD" "V101" "V102" ## [43] "V103" "V104" "V105" ## [46] "V106" "V107" "V113" ## [49] "V115" "V116" "V119" ## [52] "V120" "V121" "V122" ## [55] "V123" "V124" "V125" ## [58] "V127" "V128" "V129" ## [61] "V130" "V131" "V133" ## [64] "V134" "V135" "V136" ## [67] "V137" "V138" "V139" ## [70] "V140" "V141" "V149" ## [73] "V150" "V151" "V152" ## [76] "V153" "AWFACTT" "AWFACTU" ## [79] "AWFACTR" "AWFACTE" "AWFACTW" ## [82] "V155" "V156" "V157" ## [85] "V158" "V159" "V160" ## [88] "V161" "V166" "V167" ## [91] "V168" "ML101" "QD333_1" ## [94] "QD333_2" "QD333_3" "QD333_4" ## [97] "QD333_5" "QD333_6" "UBIGEO" ## [100] "V022" "V005" "V190" ## [103] "V191" "mujeres12a49" "NCONGLOME" ## [106] "V201" "V202" "V203" ## [109] "V204" "V205" "V206" ## [112] "V207" "V208" "V209" ## [115] "V210" "V211" "V212" ## [118] "V213" "V214" "V215" ## [121] "V216" "V217" "V218" ## [124] "V219" "V220" "V221" ## [127] "V222" "V223" "V224" ## [130] "V225" "V226" "V227" ## [133] "V228" "V229" "V230" ## [136] "V231" "V232" "V233" ## [139] "V234" "V235" "V237" ## [142] "V238" "V239" "V240" ## [145] "V241" "V242" "V243" ## [148] "V301" "V302" "V310" ## [151] "V311" "V312" "V313" ## [154] "V315" "V316" "V317" ## [157] "V318" "V319" "V320" ## [160] "V321" "V322" "V323" ## [163] "V323A" "V325A" "V326" ## [166] "V327" "V337" "V359" ## [169] "V360" "V361" "V362" ## [172] "V363" "V364" "V367" ## [175] "V372" "V372A" "V375A" ## [178] "V376" "V376A" "V379" ## [181] "V380" "V384A" "V384B" ## [184] "V384C" "V393" "V394" ## [187] "V395" "V3A00A" "V3A00B" ## [190] "V3A00C" "V3A00D" "V3A00E" ## [193] "V3A00F" "V3A00G" "V3A00H" ## [196] "V3A00I" "V3A00J" "V3A00K" ## [199] "V3A00L" "V3A00M" "V3A00N" ## [202] "V3A00O" "V3A00P" "V3A00Q" ## [205] "V3A00R" "V3A00S" "V3A00T" ## [208] "V3A00U" "V3A00V" "V3A00W" ## [211] "V3A00X" "V3A00Y" "V3A00Z" ## [214] "V3A01" "V3A02" "V3A03" ## [217] "V3A04" "V3A05" "V3A06" ## [220] "V3A07" "V3A08A" "V3A08B" ## [223] "V3A08C" "V3A08D" "V3A08E" ## [226] "V3A08F" "V3A08G" "V3A08H" ## [229] "V3A08I" "V3A08J" "V3A08K" ## [232] "V3A08L" "V3A08M" "V3A08N" ## [235] "V3A08O" "V3A08P" "V3A08Q" ## [238] "V3A08R" "V3A08S" "V3A08T" ## [241] "V3A08U" "V3A08V" "V3A08W" ## [244] "V3A08X" "V3A08Z" "V3A09A" ## [247] "V3A09B" "V305_01" "V305_02" ## [250] "V305_03" "V305_05" "V305_06" ## [253] "V305_07" "V305_08" "V305_09" ## [256] "V305_10" "V305_11" "V305_13" ## [259] "V305_14" "V305_15" "V305_16" ## [262] "V307_01" "V307_02" "V307_03" ## [265] "V307_04" "V307_05" "V307_06" ## [268] "V307_07" "V307_08" "V307_09" ## [271] "V307_10" "V307_11" "V307_12" ## [274] "V307_13" "V307_14" "V307_15" ## [277] "V307_16" "QI302_05A" "QI302_05B" ## [280] "V501" "V502" "V503" ## [283] "V504" "V505" "V506" ## [286] "V507" "V508" "V509" ## [289] "V510" "V511" "V512" ## [292] "V513" "V525" "V527" ## [295] "V528" "V529" "V530" ## [298] "V531" "V532" "V535" ## [301] "V536" "V537" "V538" ## [304] "V539" "V540" "V541" ## [307] "V602" "V603" "V604" ## [310] "V605" "V613" "V614" ## [313] "V616" "V621" "V623" ## [316] "V624" "V625" "V626" ## [319] "V627" "V628" "V629" ## [322] "V631" "V632" "V633A" ## [325] "V633B" "V633C" "V633D" ## [328] "V633E" "V633F" "V633G" ## [331] "V634" "V701" "V702" ## [334] "V704" "V705" "V714" ## [337] "V714A" "V715" "V716" ## [340] "V717" "V719" "V721" ## [343] "V729" "V730" "V731" ## [346] "V732" "V739" "V740" ## [349] "V741" "V743A" "V743B" ## [352] "V743C" "V743D" "V743E" ## [355] "V743F" "V744A" "V744B" ## [358] "V744C" "V744D" "V744E" ## [361] "V746" "peso" "moderno"Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
{survey}
Diseño de la encuesta
Tabulaciones
Tabulaciones cruzadas
Modelos
Más extenso aquí
- Las funciones de
surveyempiezan siempre consvyy exigen un objeto de encuesta con diseño. - Exigen también una fórmula, en general
~nombre. - Al resultado se le pueden pedir otras estimaciones, por ejemplo el error estándar (
SE) o el intervalo de confianza (confint) - Por defecto utiliza el intervalo al 95%. Se puede cambiar con
level.
svymean(~moderno,disDHS)## mean SE## modernoNo 0.60678 0.0055## modernoSi 0.39322 0.0055svymean(~moderno,disDHS) %>% confint()## 2.5 % 97.5 %## modernoNo 0.5959328 0.6176296## modernoSi 0.3823704 0.4040672- La función
svymeansirve para variables factor o cuantitativa, pero no tiene en cuenta que se trata de una probabilidad de una binomial. svyciprop, en cambio, sólo sirve para proporciones.- Se basa, por defecto, en el cálculo de un modelo logit.
- En este caso, no hay cambios, pero sí los hay para probabilidades cercanas a 0 o a 1.
svyciprop(~moderno,disDHS)## 2.5% 97.5%## moderno 0.393 0.382 0.4svyciprop(~moderno,disDHS) %>% SE()## as.numeric(moderno) ## 0.005535006Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
{survey}
Diseño de la encuesta
Tabulaciones
Tabulaciones cruzadas
Modelos
Más extenso aquí
Calcula la tabla, pero no utiliza etiquetas.
tabRes=svytable(~moderno+V025,disDHS)tabRes## V025## moderno 1 2## No 16651.42 3603.89## Si 10922.86 2203.40Para utilizar etiquetas hay que convertir en factor
svytable(~moderno+as_factor(V025),disDHS)## as_factor(V025)## moderno Urbano Rural## No 16651.42 3603.89## Si 10922.86 2203.40- Se pueden calcular distintas medidas de asociación entre variables, siempre teniendo en cuenta la estructura compleja.
tabRes %>% summary(statistic="Chisq")## V025## moderno 1 2## No 16651 3604## Si 10923 2203## ## Pearson's X^2: Rao & Scott adjustment## ## data: svychisq(~moderno + V025, design = disDHS, statistic = "Chisq")## X-squared = 5.5988, df = 1, p-value = 0.09966- Análogo al
group_byde {tidyverse}, podemos definir las proporciones para cada nivel o los errores estándar.
svyby(~moderno,~V501,disDHS,svymean,vartype="ci") %>% mutate(V501=as_factor(V501)) %>% kable(digits=3)| V501 | modernoNo | modernoSi | ci_l.modernoNo | ci_l.modernoSi | ci_u.modernoNo | ci_u.modernoSi | |
|---|---|---|---|---|---|---|---|
| 0 | Nunca casada | 0.850 | 0.150 | 0.835 | 0.135 | 0.865 | 0.165 |
| 1 | Casado | 0.450 | 0.550 | 0.425 | 0.525 | 0.475 | 0.575 |
| 2 | Viviendo juntos | 0.442 | 0.558 | 0.426 | 0.542 | 0.458 | 0.574 |
| 3 | Viuda | 0.812 | 0.188 | 0.688 | 0.064 | 0.936 | 0.312 |
| 4 | Divorciada | 0.703 | 0.297 | 0.475 | 0.070 | 0.930 | 0.525 |
| 5 | No viven juntos | 0.704 | 0.296 | 0.675 | 0.267 | 0.733 | 0.325 |
- Podemos convertir los objetos en
tibblesque manipulamos con las funciones del{tidyverse}
svyby(~moderno,~as_factor(V501),disDHS,svymean,vartype="ci") %>% as_tibble() %>% dplyr::select(`Estado Civil`=1,ends_with("Si")) %>% kable()| Estado Civil | modernoSi | ci_l.modernoSi | ci_u.modernoSi |
|---|---|---|---|
| Nunca casada | 0.1498518 | 0.1347637 | 0.1649398 |
| Casado | 0.5500164 | 0.5252821 | 0.5747506 |
| Viviendo juntos | 0.5582293 | 0.5422314 | 0.5742272 |
| Viuda | 0.1879977 | 0.0643558 | 0.3116396 |
| Divorciada | 0.2973546 | 0.0698621 | 0.5248470 |
| No viven juntos | 0.2957780 | 0.2667916 | 0.3247644 |
Ejemplo:
Uso de anticonceptivos en la ENDES-DHS Perú 2019
{survey}
Diseño de la encuesta
Tabulaciones
Tabulaciones cruzadas
Modelos
Más extenso aquí
- Vamos a estimar el modelo logit de
modernoen función de residencia y estado civil. - Transformamos primero las variables V025 y V501 en factores.
updatees equivalente amutatepero en objetossvy.
disDHS2=update(disDHS,`Estado civil`= as_factor(V501), Residencia=as_factor(V025))Paquetes útiles para transformar:
{stringr}, cadenas; {forcats}, {labelled} y {sjmisc}, factores, NAs.
as_factor, to_factor, unlabelled, to_character
svyglmfunciona igual queglm, pero no hace falta explicitar pesos o conglomerados al estar declarados en el diseño.
mod3= svyglm(moderno~`Estado civil`+Residencia, disDHS2, family=binomial())summary(mod3)## ## Call:## svyglm(formula = moderno ~ `Estado civil` + Residencia, design = disDHS2, ## family = binomial())## ## Survey design:## update(disDHS, `Estado civil` = as_factor(V501), Residencia = as_factor(V025))## ## Coefficients:## Estimate Std. Error t value## (Intercept) -1.69444 0.06116 -27.703## `Estado civil`Casado 1.97260 0.08028 24.570## `Estado civil`Viviendo juntos 2.01942 0.06941 29.094## `Estado civil`Viuda 0.36503 0.42723 0.854## `Estado civil`Divorciada 0.83638 0.56275 1.486## `Estado civil`No viven juntos 0.86484 0.09150 9.452## ResidenciaRural -0.38665 0.04603 -8.400## Pr(>|t|) ## (Intercept) <2e-16 ***## `Estado civil`Casado <2e-16 ***## `Estado civil`Viviendo juntos <2e-16 ***## `Estado civil`Viuda 0.393 ## `Estado civil`Divorciada 0.137 ## `Estado civil`No viven juntos <2e-16 ***## ResidenciaRural <2e-16 ***## ---## Signif. codes: ## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 0.9975517)## ## Number of Fisher Scoring iterations: 4mod3 %>% sjPlot::tab_model()| moderno | |||
|---|---|---|---|
| Predictors | Odds Ratios | CI | p |
| (Intercept) | 0.18 | 0.16 – 0.21 | <0.001 |
| Estado civil actual: Casado |
7.19 | 6.14 – 8.41 | <0.001 |
| Estado civil actual: Viviendo juntos |
7.53 | 6.58 – 8.63 | <0.001 |
| Estado civil actual: Viuda |
1.44 | 0.62 – 3.33 | 0.393 |
| Estado civil actual: Divorciada |
2.31 | 0.77 – 6.95 | 0.137 |
| Estado civil actual: No viven juntos |
2.37 | 1.98 – 2.84 | <0.001 |
| Tipo de lugar de residencia: Rural |
0.68 | 0.62 – 0.74 | <0.001 |
| Observations | 33311 | ||
| R2 / R2 adjusted | 0.118 / -8.796 | ||
plot3= mod3 %>% sjPlot::plot_model(show.values=TRUE)plot3+theme_bw(18)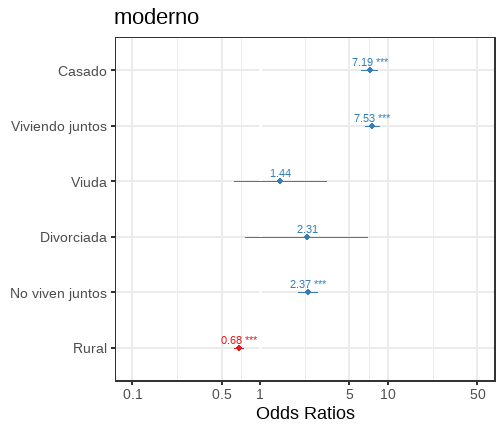
mod3 %>% broom::glance()## # A tibble: 1 x 6## null.deviance df.null AIC BIC deviance df.residual## <dbl> <int> <dbl> <dbl> <dbl> <dbl>## 1 44648. 33310 39416. 39439. 39366. 2998mod3 %>% broom::tidy() %>% knitr::kable(digits=3)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -1.694 | 0.061 | -27.703 | 0.000 |
Estado civilCasado |
1.973 | 0.080 | 24.570 | 0.000 |
Estado civilViviendo juntos |
2.019 | 0.069 | 29.094 | 0.000 |
Estado civilViuda |
0.365 | 0.427 | 0.854 | 0.393 |
Estado civilDivorciada |
0.836 | 0.563 | 1.486 | 0.137 |
Estado civilNo viven juntos |
0.865 | 0.092 | 9.452 | 0.000 |
| ResidenciaRural | -0.387 | 0.046 | -8.400 | 0.000 |
¿Y qué pasa si no tengo en cuenta el diseño complejo? El efecto del diseño.
Subestimación de la variabilidad
- Si no tenemos en cuenta el diseño complejo subestimamos la variabilidad de nuestros estimadores.
- Pensaremos que nuestros estimadores son más precisos de lo que son, los intervalos de confianza serán demasiado estrechos, y los contrastes producirán p-valores demasiado pequeños.
- Al cociente entre la varianza muestral correcta y la que asume muestreo aleatorio se le denomina efecto del diseño
- El paquete
{survey}permite calcularlo directamente ensvymean. También lo podemos calcular especificando diseños alternativos. - Valores típicos ~4 (doble SE).
svymean(~moderno,disDHS2,deff="replace")## mean SE DEff## modernoNo 0.606781 0.005535 4.2771## modernoSi 0.393219 0.005535 4.2771Los errores estándar son más del doble de los que se calcularían bajo muestreo aleatorio, la varianza más del cuádruple.
# Diseño sin uso de pesosDHSunw=svydesign(ids=~1,strata=NULL,weights=NULL, data=DHS %>% filter(peso>0,!is.na(moderno)))# Diseño con pesos pero sin estructura complejaDHSw=svydesign(ids=~1,strata=NULL,weights=~peso, data=DHS %>% filter(peso>0,!is.na(moderno)))SE_comp=svyciprop(~moderno,disDHS) %>% SE()SE_w= svyciprop(~moderno,DHSw) %>% SE()SE_unw= svyciprop(~moderno,DHSunw) %>% SE()tribble(~Método,~SE, "Encuesta Compleja",SE_comp, "Con pesos",SE_w, "Sin pesos",SE_unw) %>% mutate(var=SE^2,deff=var/last(var)) %>% kable(digits=6)| Método | SE | var | deff |
|---|---|---|---|
| Encuesta Compleja | 0.005535 | 3.1e-05 | 4.107447 |
| Con pesos | 0.005215 | 2.7e-05 | 3.646239 |
| Sin pesos | 0.002731 | 7.0e-06 | 1.000000 |
- La parte más grande del efecto del diseño se capta utilizando pesos.
- En EncuestaR2 también se presenta cómo usar
vcovCL.
Conclusiones: Buenas prácticas con datos de encuesta en R
Buenas prácticas con datos de encuesta.
IMPORTAR:
Con {haven}. Si da problemas, {memisc}
TABLAS:
Con {sjmisc}, fácil, o {expss}, potente. Con pesos.
MODELOS
Transformar primero variables a factores o numéricas
MODELOS ESTÁNDAR:
Declarar diseño y estimar con {survey}. Tablas y gráficos con {sjPlot}
MODELOS NO DISPONIBLES EN SURVEY:
Con el paquete correspondiente. Usar pesos y varianzas cluster.
Referencias
Ejemplos más extensos, con referencias abundantes:
Ortega, J. A. (2020a) Lectura de encuestas INE y análisis microeconométrico, EncuestaR - Análisis de Encuestas con R. Curso del Doctorado en Economía 2020-21. Universidad de Salamanca. https://rpubs.com/jaortega/EncuestaR1
Ortega, J. A. (2020b) Análisis de encuestas complejas con survey. EncuestaR - Análisis de Encuestas con R. Curso del Doctorado en Economía 2020-21. Universidad de Salamanca. https://rpubs.com/jaortega/EncuestaR2
Ejemplos de código para encuestas internacionales:
Damico, A. J. (2020) “Analyze survey data for free”, http://asdfree.com/

¡Gracias!


